Τhe Antikythera Mechanism:
a Computer Science Perspective

Diomidis Spinellis[1]

Two thousand years separate us from an ancient Greek computing device known as the “Mechanism of Antikythera”.   Here I explain the mechanism’s operation based on its reconstruction in the Squeak EToys environment.^1,2  The reconstruction relies on the recent findings that an international cross-disciplinary team of scientists obtained through surface imaging and high-resolution X-ray tomography.  My work aims to present the functioning of this remarkable device using working code, the language of our community.

The complete image of this implementation of the Antikythera Mechanism implementation is available online as open-source software running on the EToys environment (www.dmst.aueb.gr/dds/sw/ameso/).  I encourage this article’s readers to download an EToys image and run the software on it, as they step through the descriptions in the text.  I will report on the educational significance of the implementation platform I chose and the methods used for implementing the mechanism in a separate paper.

History

In 1900 a group of sponge-fishers seeking shelter from the cruel weather of the Kythera Sea anchored their boats on a the barren island of Antikythera.  Diving there they discovered at a depth of 42 meters an ancient ship-wreck carrying bronze and marble statues.   For almost a year afterwards they worked with the Greek government salvaging the ship’s contents.  These were then transferred for preservation and study to the Greek Archeological museum, where we can see them to this day.   The items found were dated in the first century B.C.  Among them were a beautiful nude bronze statue and a severely corroded lump of bronze containing what were clearly gear-wheels.

A number of scientists have devoted their life to the study of this mysterious mechanism.  The first theories were based on the few letters that could be read on the fragments and descriptions of mechanical contraptions in ancient Greek and Roman texts.  Thus the device was variously identified as an astrolabe or a planetarium.  The historian of science Derek de Solla Price, also known as the father of scientometrics, spent three decades analyzing and reconstructing the device.  By using radiographs he was able to count the teeth of most of the device’s gears and construct a detailed model of their operation.³  In his seminal monograph, published in 1974, he described the mechanism as a calendar computer. Famously, his proposed model included a differential mechanism, similar to the one found in the drive trains of modern cars, apparently constructed scores of centuries before its reinvention.

Recently, astronomers, archeologists, computer engineers, and physicists from around the world collaborated to reconstruct a different and more precise model of the mechanism.⁴  Their 35-gear model accounts for all but one of the 30 gears found in its fragments.  The study was based on three computer-based imaging techniques: three-dimensional X-ray microfocus computed tomography, polynomial texture mapping, and digitized high-quality photography.  These techniques allowed the detailed study of virtual cross-sections of the device under various (simulated) lighting conditions.  Some spectacular samples of the images are available for interactive study on the web (www.antikythera-mechanism.gr/).  The study confirmed that the device was indeed a calendar computer.  However, the new model proposes that the gears that Price identified as a differential work in a different, but no less sophisticated, manner to model the anomaly in the Moon’s rotation.

Calculating with Gears

 

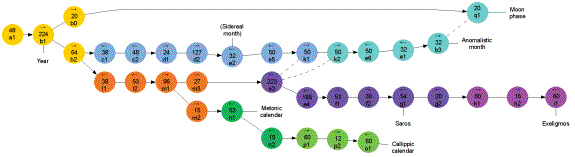
Figure 1 The gears of the Antikythera Mechanism operational model

The model of the Antikythera Mechanism I will present consists of 35 gears.  Archeologists have been identified 30 in the surviving fragments, while the science historian Michael Wright and the multidisciplinary group I referred to above have introduced another five to explain the device’s functionality.^4,5  You can see the relationships of all the years as a graph in Figure 1.  Each circle in the figure represents one gear. The arrow on the top shows the direction the gear is turning: → for clockwise, and ← for counter-clockwise.  The number of teeth on the gear appears in the center.  In all studies gears are named systematically with a letter-number combination: gears with the same letter are concentric; the numbers increase from the front to the back of the mechanism.   In my figure I’ve followed the naming and coloring nomenclature adopted in the 2006 Nature article.⁴  Gears either rotate together as one piece, and are shown in the figure connected with a simple line, or they engage other gears through their teeth and are shown connected with an arrow.   By making a pair of gears with your hands (using your fingers as teeth) you can easily verify that when two gears engage their direction of rotation reverses.  You can see the same effect throughout  the gear diagram.

Let us now examine how gears are used to perform calculations.  Whenever two gears engage through their teeth (for example b2 with c1) their ratio of rotation periods will equal the ratio of their teeth.  Thus in our example, b2 will complete one rotation in 64 time units, whereas c1 will complete one rotation 38 time units.  Concentric gears rotating together have by defintion the same rotation period.  Therefore we can obtain the ratio derived by a sequence of rotating gears by multiplying together the ratios of all engaged gears.

 

Figure 2 The mechanism's front dial (left) and back dial (right)

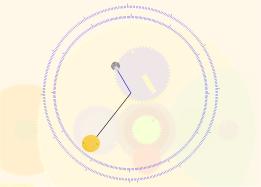
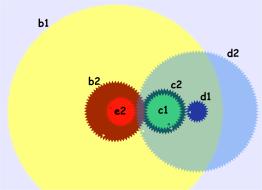
The input to the Antikythera Mechanism is controlled through gear a1, which engaged laterally with gear b1, and could conceivably be rotated with a hand-crank.  However, the actual value of the mechanism’s input appears through gear b1, which, through a dial residing on the front face of the mechanism, shows the Sun’s position throughout the year on the Zodiac cycle and a 365-day calendar (see Figure 2).  The calendar’s scale can be rotated by one day every four years to take into account leap years.  The known computed outputs of the mechanism are

• the position and phase of the Moon (also appearing on the front face),
• a so-called luni-solar calendar (based on lunar months), and
• a prediction of eclipses.

The luni-solar calendar and the eclipse prediction dials appear on the device’s back face.  All dials rotate clockwise, and this is why on  Figure 1 the gears driving the back-face dials rotate counter-clockwise.  I will begin the description of the individual elements from the two back-face elements, because these are the most straightforward.

The Luni-solar Calendar

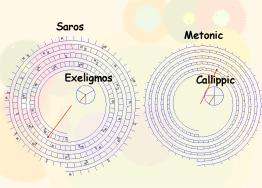
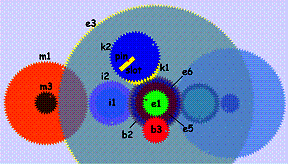
Reckoning time progression through the Moon’s phases is convenient.  It involves a calendar based on recurring Moon phases defining the 29 ½ day so-called synodic month—the time, for instance, from one full moon to the next.  However, the months of such a calendar don’t fit correctly in the seasonal year, which has practical significance for, say, agriculture.  The Athenian astronomer Meton devised a way around this problem, by observing that 19 seasonal (known as tropical) years contain almost exactly 235 synodic months, and proposing a cycle containing 125 full months of 30 days and 110 hollow, 29 day, months.⁶  A century later Callippus further refined that model by proposing the removal of one day every four Metonic cycles.  Two dials on the back of the Antikythera Mechanism indicate the length of each month in a Metonic cycle, and also track the progress through the Callippic cycle. 

To increase the “resolution” of the Metonic display, the Metonic dial rotates five times in each cycle with a pointer tracking a five-turn spiral.  You can see that setup in Figure 2 (right).  As the pointer rotates, the spiral’s grooves force it to move toward the outer turns of the spiral, in a way similar to that of a needle tracking a gramophone record.  Once the pointer reached the end of the spiral the human operator would presumably return it back to the beginning.

Figure 3 The gears for the luni-solar calendar (left) and eclipse prediction (right)

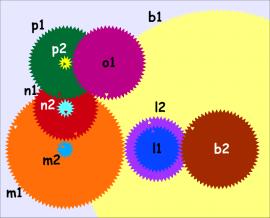
From the previous description it follows that gear n2 driving the dial of the Metonic calendar must rotate 5 times in 19 years, so the ratio between the gear b1 tracking the tropical years and n2 should be 5/19.  Indeed the sequence b2-l1-l2-m1-m2-n1 calculates this ratio: 64/38 * 53/96 * 15/53 = 960/3648 = 5/19.  Furthermore, gear o2 driving the dial of the Callippic cycle must turn at a ratio 1/20 of the Metonic dial: once every 4 cycles of 5 turns each.  The sequence n2-p1-p2-o1 calculates the required ratio: 15/60 * 12/60 = 1/20.  You can see the emulator setup of these gears in Figure 3 (left).

Eclipse Prediction

The Antikythera Mechanism predicts eclipses by means of the Saros cycle established by the ancient Babylonian astronomers: a period of 223 ⅓ synodic months in which identical Moon and Sun eclipses occur.  Glyphs on the 223 month divisions of the plate where the Saros dial rotates indicate type of each eclipse.  The letter Σ (ΣΕΛΗΝΗ—Moon) indicates a lunar eclipse, while the letter Η (ΗΛΙΟΣ—Sun)  a solar one.  In common with the Metonic display, the Saros display is also laid out in a four-turn spiral.  Fascinatingly, the construction of the Saros display involves two elements of modern software engineering: the use of a lookup table (the Saros eclipse data) to aid computation, and the adoption of a design pattern (a spiral for increasing the display’s resolution).  Because the Saros cycle contains a ⅓ day fraction, one has to wait three Saros cycles in order to witness an eclipse at the same time.  Thus a separate dial indicates the Exeligmos cycle, which comprises three Saros cycles, and can be used to predict the time of each eclipse.

The emulator setup of the eclipse prediction gears appears in Figure 3 (left).  We already know from the Metonic calendar that there are 235 synodic months in 19 years.  For the Saros display we need four revolutions in 223 synodic months, a ratio of 4/223 * 235/19.  The sequence b2-l1-l2-m1-m3-e3-e4-f1-f2-g1 establishes this ratio (you can easily verify this with a calculator).  Furthermore, the Exeligmos dial must turn once every three four-turn Saros cycles, therefore at a rate 1/12 of Saros.  This is calculated through the sequence g2-h1-h2-i1.

Lunar Calculations

Figure 4 The calculation of the sidereal month (left) and its modification by Hipparchos’ lunar mechanism (right)

The Moon’s position is indicated on the front dial as the anomalistic month: the position of the Moon on the celestial sphere taking into account the Moon’s elliptic orbit, and the additional rotation of the ellipse’s two extreme points.  This anomaly is caused by the solar tide, and one full rotation takes nine years to complete.  Gears b0 and q1 combine the Moon’s position with that of the Sun to show the phase of the Moon.  The calculation of the Moon’s position is the most sophisticated calculation of the known parts of the mechanism.  I will describe it in three steps.

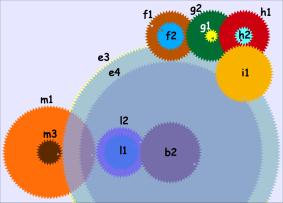
The first step involves the calculation of the so-called sidereal month: the period of the Moon in a fixed frame of reference.  In a period of 19 years the Moon will have  performed the 235 synodic rotations I described earlier and another 19 due to its rotation around the Sun; a total of 254.  The required yearly rotation ratio 254/19 is calculated through the sequence b2-c1-c2-d1-d2-e2, shown in Figure 4 (left).

The mechanism models the Moon’s elliptical orbit through an ingenious device.  The sidereal rotation established on gear e2 is transferred up to gear e5, which is mounted on the same axle (see the right side of Figure 4).  Gear e5 turns k1, which has a pin mounted a small distance from its center.  Gear k2 is mounted below k1, but its center is slightly displaced from the center of k1.  The pin moves within a slot cut into gear k2, and, because the two gears are eccentrically mounted, harmonically varies k2’s rotation rate.  By running the Antikythera emulator you can see that the rotational speed of k2 is high when the slot is at the top of the screen and low when it is at the bottom; this models the corresponding variation of the Moon’s speed between its perigee and apogee.

Finally, the mechanism models the rotation of this elliptical orbit, by having k1 and k2 mounted on e3.  The gear e3 rotates at the rate of the elliptical orbit’s rotation (the precession period of the Moon’s long axis) through the sequence b2-l1-l2-m1-m3-e3. Note that this rotates k2’s axis, and complicates driving a dial with it.  Therefore, k2 drives e6, which is on a fixed axis.  Gear e6 drives e1, which is located on the front-dial side of e3, and b3 moves the rotation clockwise to the front-dial’s center.  A computer engineer would say that the sequence e6-e1-b3 interfaces the processing unit to the display unit.

Another parallel with modern computing technology is the dual role of some gears: e3 in the calculation of both the Saros and the anomalistic month, and m1 in the calculation of Saros and the luni-solar calendar.  This is a technique commonly employed in digital circuits; for example, in a full adder implementation the half-adder sum output typically drives both the sum and the carry bit circuits.

Implementation Notes

One can find on the web a number of Antikythera Mechanism simulators.  These replicate the mechanism’s operation in software using computer arithmetic to simulate the gear interactions, and then reflect back the computed results onto the simulated gears.  In addition, these simulators are based on the outdated Price’s model.  In contrast my implementation is an emulator design of the modern model.  The emulator doesn’t calculate the gear positions. Instead, it employs mechanical principles (gear teeth pushing each other) to emulate the mechanism at a physical level.

This approach allowed me to experience the physical properties of the mechanism and appreciate the thinking of its ancient developer(s).  It also fitted neatly with  of the constructivist learning approach of the EToys platform I used.

EToys programming is based on assembling together primitives that manipulate visual objects appearing on the screen.  The intellectual forebears of EToys are Logo, Smalltalk, and HyperCard.  It is currently used as a teaching vehicle in high schools in Asia, Europe, Japan, South America, and the United States.  It is also an integral part of the One Laptop Per Child Initiative, XO computer, also known as the $100 laptop.

Each gear and dial appearing on the screen is a separate object.  Although the gears may look formidable, building them was simple:  I constructed them as polygons, tooth by tooth.  I started with an empty polygon.  After I added the tooth’s two vertices, I rotated the gear by the tooth’s displacement, and repeated the operation.  This mode of construction resembles the manual cutting of physical gear teeth.  Having the gears as polygons makes modeling their interactions a child’s play.  EToys has a built-in primitive to locate overlapping objects.  Thus, on each time step I simply look for overlapping polygons and rotate them in the appropriate direction.

I used a similar principle for implementing the pointer-follower mechanism of the spiral dials, and the pin and slot device of Hipparchos’s lunar mechanism.  The emulated back-face dials contain a small circular pin at their end that traces the spirals.  When the pin overlaps with the spiral’s edge, I simply increase the dial’s length, and move the pin to its new end.  To implement Hipparchos’s lunar mechanism I bore a hole on the polygon of gear k2, by adding 6 more vertices.  The pin is a separate object, which I rotate in sync with k1.  Whenever the pin overlaps k2, k2 rotates, thus responding to k1’s “push”.

For the sake of simplicity the emulation and the corresponding images in this article depart from the actual construction in a few ways.  First, the positioning of the gears and the dials doesn’t follow the mechanism’s actual layout, because positioning gears on the horizontal and vertical axes is significantly simpler, and also makes the gears’ operation easier to inspect.  Furthermore, although in the mechanical operation as gears engage their direction reverses, in my implementation I hard-coded the appropriate new direction in each gear engagement test.

Finally, in contrast to the actual mechanism, in my implementation the ratio of gear teeth to gear diameter is constant.  Because, I had already simplified the gear layout, I didn’t see any point in following in my emulation the exact gear dimensions. The fixed-sized teeth and the liberties I’ve taken with the placement of gears result in some gears that should be mounted on the same axis appearing in places different from the original.  In the emulator, this isn’t a problem, because I implement gears mounted on top of each other by simply maintaining them on the same heading after each gear rotation.  In the actual mechanism varying teeth sizes allow gear rotations representing different calculated values to appear on the same axis for further processing.

For instance, in the original mechanism the sequence b2-i1-i2-m1-m3-e3 representing the rotation of the Moon’s orbit line of apses (perigee and apogee) shares the same axis with the sequence b2-c1-c2-d1-d2-e2 representing a sidereal month.  This allows the two quantities to be subtracted (through the epicyclical mounting of k1 and k2) in order to calculate the moon’s eccentric motion at the required rate of the anomalistic month.

Here, we can draw an enticing analogy with hardware construction for high-speed computers.  The mechanism employs different gear sizes to drive two separate quantities to the same axis.  In a similar manner modern printed circuit board design software will route separate but related signal paths in a way that will keep their length equal, so that the signals will arrive concurrently at their destination for further processing. 

Lessons Learned

I’ve not regretted choosing emulation over simulation and adopting the EToys platform as base for this model of the Antikythera Mechanism.  For instance, the faithful emulation of the device revealed two bugs that would have otherwise gone unnoticed.  My first operation of the back-face dials had the Saros dial scan months at a different rate than the Metonic dial.  Normally both should move through lunar months at exactly the same rate: 235 months every 19 years.  Furthermore the Callippic dial appeared to be moving too slowly.  By examining the number of teeth I had programmed in each gear I found that gear p2 had 15 teeth instead of 12, and gear g1 60 teeth instead of 54.  This accident demonstrates that by emulating the mechanism we can actually validate its operation.

Scientific and engineering visualization applications can be a tough nut to crack, and have attracted the attention of many influential researchers.^7,8  The disparate phenomena we want to show do not allow us to standardize to a specific presentation format.  Therefore, we can’t use cookie-cutter techniques and implementation frameworks, such as those available for implementing desktop applications.  Moreover, when we deal with educational applications we also want to make their implementation accessible to students, avoiding complex algorithms, formulas, or implementation techniques.  Having experimented with other candidate environments, like Visual Basic and Tcl/Tk, I can vouch that in its niche EToys currently holds a significant edge.  Adopting it made the development of the Antikythera Mechanism emulator a productive, accessible, and enjoyable activity.  It also allowed me to appreciate the mechanism’s beauty, and, dare I say it, I times talk with that unknown computer engineer who two millennia ago was grappling with similar problems.

References

1.       Dan Ingalls, Ted Kaehler, John Maloney,  Scott Wallace, and Alan Kay. Back to the future: the story of Squeak, a  practical Smalltalk written in itself. In OOPSLA '97: Proceedings of  the 12th ACM SIGPLAN conference on Object-oriented programming, systems,  languages, and applications, pages 318–326, New York, NY, USA, 1997.  ACM Press.

2.       M. Gaelli, O. Nierstrasz, and  S. Stinckwich. Idioms for composing games with EToys. In Creating,  Connecting and Collaborating through Computing, 2006. C5 '06. The Fourth  International Conference on, pages 222–231, 2006.

3.       Derek de Solla Price. Gears from the  Greeks: The Antikythera Mechanism — a calendar computer from ca. 80  B.C. Transactions of the American Philosophical Society — New  Series, 64(7), November 1974.

4.       T. Freeth, Y. Bitsakis, X. Moussas,  J. H. Seiradakis, A. Tselikas, H. Mangou, M. Zafeiropoulou, R. Hadland,  D. Bate, A. Ramsey, M. Allen, A. Crawley, P. Hockley, T. Malzbender,  D. Gelb, W. Ambrisco, and M. G. Edmunds. Decoding the ancient Greek  astronomical calculator known as the Antikythera Mechanism. Nature,  444(7119):587–591, November 2006.

5.       M. T. Wright. The Antikythera  mechanism: A new gearing scheme. Bulletin of the Scientific Instrument  Society, 85:2–7, June 2005.

6.       Nachum Dershowitz and Edward M. Reingold.  Calendrical Calculations. Cambridge University Press, Cambridge,  1997.

7.       Brian W. Kernighan. Experience with  TclTk for scientific and engineering visualization. In   Proceedings of the TclTk Workshop, pages 269–278, July  1995.

8.       Casey Reas and Ben Fry. Processing: A Programming Handbook for Visual Designers and Artists. MIT Press, 2007.

 

Acknowledgements: This work was partially funded by the European Community’s Sixth Framework Programme under the contract IST-2005-033331 “Software Quality Observatory for Open Source Software (SQO-OSS)”.  Many thanks to Tony Freeth and the team of the Antikythera Mechanism project for supplying me with a hi-resolution photo of the back dial.

 

Diomidis Spinellis is an associate professor in the Department of Management Science and Technology at the Athens University of Economics and Business and the author of Code Quality: The Open Source Perspective (Addison-Wesley, 2006). He has a PhD in computer science from Imperial College London. His research interests include software engineering and programming languages.  He is a member of the IEEE Computer Society and a senior member of the ACM.  Contact him at dds@aueb.gr.